Combinatorics

Factorial function

# Iterative
fac = fn|n|
   y = 1
   for i in 1..n
      y = y*i
   end
   return y
end


# Recursive
fac = |n| 1 if n==0 else n*fac(n-1)


# Functional
fac = |n| (1..n).reduce(1,|x,y| x*y)


# As a dynamic system
Fac = |[n,y]| [n+1,y*(n+1)]
fac = |n| (Fac^n)([0,1])[1]
fac = |n| Fac.orbit([0,1]).skip(n)()[1]


# Tail-recursive
function call(f,n,y)
   x = f(n,y)
   while x: Function
      x = x()
   end
   return x
end

Fac = |n,y| y if n==0 else || Fac(n-1,y*n)
fac = |n| call(Fac,n,1)


# Recursive, by Y combinator
Y = |F| (|x| x(x))(|x| F(|n| x(x)(n)))
fac = Y(|f||n| 1 if n==0 else n*f(n-1))


# Corecursive
fac = |n| fn*||
   y=1; k=1
   while true
      yield y
      y, k = y*k, k+1
   end
end.skip(n)()


# By counting all permutations inside of the
# space of all mappings from 0..n-1 to 0..n-1
fac = |n| (list(n)^n).count(|t| (0..n-1).all(|x| x in t))


# By generating all permutations and counting them
use itertools: permutations
fac = |n| permutations(n).count()


# Print them to the terminal
(0..9).map(|n| [n,fac(n)]).each(print)

Permutations

# Generate all permutations of a list
function permutations(a)
   if len(a)<=1
      return [copy(a)]
   else
      b = []
      x = a[..0]
      for p in permutations(a[1..])
         for i in 0..len(a)-1
            b.push(p[..i-1]+x+p[i..])
         end
      end
      return b
   end
end


# Return an interator instead of a list
function permutations(a)
   return fn*||
      if len(a)<=1
         yield copy(a)
      else
         x = a[..0]
         for p in permutations(a[1..])
            for i in 0..len(a)-1
               yield p[..i-1]+x+p[i..]
            end
         end
      end
   end
end

for n in 0..4
   permutations(list(n)).each(print)
end


# Generate all permutations of an ordered
# list in lexicographical order
function permutations(a)
   if len(a)==0
      return [[]]
   else
      b = []
      for i in 0..len(a)-1
         for x in permutations(a[..i-1]+a[i+1..])
            b.push([a[i]]+x)
         end
      end
      return b
   end
end

# Return an iterator instead of a list
function permutations(a)
   return fn*||
      if len(a)==0
         yield []
      else
         for i in 0..len(a)-1
            for x in permutations(a[..i-1]+a[i+1..])
               yield [a[i]]+x
            end
         end
      end
   end
end


# Take any iterable
perm = |a| permutations(list(a))

k-Permutations

# Generate all k-permutations of an ordered
# list in lexicographical order
perm = |a,k=len(a)| [[]] if k==0 else list([a[i]]+x
   for i in len(a) for x in perm(a[..i-1]+a[i+1..],k-1))

Cartesian product

# as a list
prod = |*a| [[]] if a==[] else list(
   [x]+t for x in a[0] for t in prod(*a[1..]))
  
# as a set
prod = |*a| {[]} if a==[] else set(
  [x]+t for x in a[0] for t in prod(*a[1..]))

# as an iterator
prod = |*a| iter([[]]) if a==[] else (
  [x]+t for x in a[0] for t in prod(*a[1..]))

# as a list
prod = |*a| a.reduce([[]],|x,y| (x*list(y)).map(|[t,s]| t+[s]))

Bernoulli numbers

There is a recursive formula for the Bernoulli numbers:

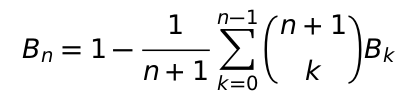
This formula can be implemented directly, taking advantage of exact rational numbers in combination with long integers.

# memoizing fixed point combinator
use functional: fix

# rational numbers
use math.rational: rat

# binomial coefficient
use math.cf: bc


B = fix({},|B,n| 1 if n==0 else
  1-rat(1,n+1)*(0..n-1).sum(|k| B(k)*bc(n+1,k)))


for n in 0..8
   print([n,B(n)])
end
# [0, 1]
# [1, 1/2]
# [2, 1/6]
# [3, 0]
# [4, -1/30]
# [5, 0]
# [6, 1/42]
# [7, 0]
# [8, -1/30]


print(B(60))
# -1215233140483755572040304994079820246041491/56786730

Alternatively:

# factorial,
# Eulerian numbers of the first order,
# Stirling numbers of the second kind
use math.cf: fac, euler1, stirling2

B = |n| rat(
  n*(0..n-1).sum(|k| (-1)^k*euler1(n-1,k)),
  2^n*(2^n-1)
)

B = |n| (0..n).sum(|k|
  rat((-1)^k*fac(k)*stirling2(n+1,k+1),k+1))

B = |n| rat(1,2) if n==1 else (0..n).sum(|k|
  rat((-1)^k*fac(k)*stirling2(n,k),k+1))

B = |n| rat(n,2^(n+1)-2)*(0..n-1).sum(|k|
  rat(fac(k)*stirling2(n,k+1),(-2)^k))