Typen und Funktionen zwischen diesen lassen sich aus einer mathematischen Sichtweise als Kategorie betrachten. Die Typen sind hierbei Objekte der Kategorie, die Funktionen die Morphismen.
Ein Typkonstruktor F bildet zusammen mit einer
ebenfalls F genannten Abbildung höherer Ordnung
einen Funktor, sofern die beiden Regeln
F(id) = id, F(g∘f) = F(g)∘F(f)
erfüllt sind.
Der Typkonstruktor F:=Option bildet zusammen mit
seiner Methode F:=map einen Funktor. Anstelle von
map(f)(x) schreiben wir in Rust x.map(f).
Es gilt map(id) = id, denn
x.map(id)
= match x {Some(x) => Some(id(x)), None => None}
= match x {Some(x) => Some(x), None => None}
= id(x).
Zudem gilt map(g∘f) = map(g)∘map(f), denn
x.map(|x| g(f(x)))
= match x {Some(x) => Some(g(f(x))), None => None}
= match x {Some(x) => Some(f(x)).map(g), None => None}
= match x {Some(x) => Some(f(x)), None => None}.map(g)
= x.map(f).map(g).
Im Weiteren tut sich dann irgendwann die Frage auf, ob sich zum Funktor-Konzept eine Schnittstelle programmieren lässt. Bei Beschränkung auf Selbstabbildungen finden wir recht mühelos eine Umsetzung, etwa so:
trait Functor<X> {
fn map(self, f: impl Fn(X) -> X) -> Self;
}
impl<X> Functor<X> for Option<X> {
fn map(self, f: impl Fn(X) -> X) -> Self {
match self {Some(x) => Some(f(x)), None => None}
}
}
fn main() {
println!("{:?}", Functor::map(Some(0), |x| x + 1));
}
Als nächstes müssen wir uns um die Loslösung von der Beschränkung auf Selbstabbildungen kümmern. Zunächst ein Zwischenschritt:
trait Functor<X> {
fn map<Y>(self, f: impl Fn(X) -> Y) -> Option<Y>;
}
impl<X> Functor<X> for Option<X> {
fn map<Y>(self, f: impl Fn(X) -> Y) -> Option<Y> {
match self {Some(x) => Some(f(x)), None => None}
}
}
Nun stellt sich die Frage, wie man das Artefakt
Option<Y> entfernt. An dieser Stelle kommen
generische assoziierte Typen ins Spiel. Darunter versteht man
die Erweiterung des Begriffs der assoziierten Typen auf
Typkonstruktoren. Zur Notation bekommt der assoziierte Typ schlicht
einen Typparameter.
trait Functor<X> {
type F<T>: Functor<T>;
fn map<Y>(self, f: impl Fn(X) -> Y) -> Self::F<Y>;
}
impl<X> Functor<X> for Option<X> {
type F<T> = Option<T>;
fn map<Y>(self, f: impl Fn(X) -> Y) -> Self::F<Y> {
match self {Some(x) => Some(f(x)), None => None}
}
}
fn main() {
println!("{:?}", Functor::map(Some(0), |x| x + 1));
}
Warum wurde hier Fn anstelle von FnOnce
angegeben, wo die Methode Option::map doch
FnOnce bekommen darf? Die Antwort liegt in der
Komplikation, die daraus entstehen würde. Es gibt auch
Implementierungen, wo f mehrmals aufgerufen wird,
die sich bei FnOnce verbieten würden. So haben wir:
impl<X> Functor<X> for Vec<X> {
type F<T> = Vec<T>;
fn map<Y>(self, f: impl Fn(X) -> Y) -> Self::F<Y> {
self.into_iter().map(f).collect()
}
}
Der Typkonstruktor Option besitzt noch eine weitere
Eigenschaft. Durch diesen kommt jedem Typ X eine
Funktion
fn Some(x: X) -> Option<X>
zu. Die Familie dieser Funktionen ist eine sogenannte natürliche Transformation, denn
Some(f(x)) = map(f)(Some(x)),
kurz
Some∘f = map(f)∘Some,
oder abstrakt
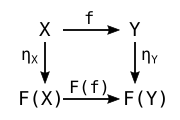
η∘f = F(f)∘η.
Übersichtlich ausgedrückt bedeutet diese Gleichung, dass das Diagramm

bzw.
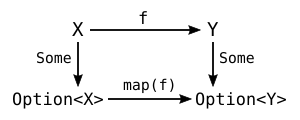
kommutiert.
Betrachten wir nochmals die Trait-Definition aus dem
Abschnitt ›Monaden‹.
Die Implementierung für Option geht so:
trait Monad<X> {
fn unit(x: X) -> Self;
fn bind(self, f: impl Fn(X) -> Self) -> Self;
}
impl<X> Monad<X> for Option<X> {
fn unit(x: X) -> Self {Some(x)}
fn bind(self, f: impl Fn(X) -> Self) -> Self {
match self {Some(x) => f(x), None => None}
}
}
fn main() {
let mx = Option::unit(0);
println!("{:?}", mx.bind(|x| Some(x + 1)));
}
Wie bei Functor würden wir die Funktionalität
gerne so verallgemeinern, dass in
f: impl Fn(X) - > Option<Y>
nicht mehr X = Y vorausgesetzt ist.
Die Umsetzung benutzt ganz analog zu der von Functor
einen generischen assoziierten Typ.
trait Monad<X> {
type M<T>: Monad<T>;
fn unit(x: X) -> Self;
fn bind<Y>(self, f: impl Fn(X) -> Self::M<Y>) -> Self::M<Y>;
}
impl<X> Monad<X> for Option<X> {
type M<T> = Option<T>;
fn unit(x: X) -> Self {Some(x)}
fn bind<Y>(self, f: impl Fn(X) -> Self::M<Y>) -> Self::M<Y> {
match self {Some(x) => f(x), None => None}
}
}
fn main() {
let mx = Option::unit(0);
println!("{:?}", mx.bind(|x| Some([x + 1, x + 2])));
}
Es verhält sich nun so, dass jede Monade auch ein Funktor ist. Wir haben nämlich
map(f)(x) = bind(unit∘f)(x),
bzw. in Rust-Schreibweise
x.map(f) = x.bind(|x| unit(f(x))).
Die allgemeine Implementierung:
impl<X, M: Monad<X>> Functor<X> for M {
type F<T> = M::M<T>;
fn map<Y>(self, f: impl Fn(X) -> Y) -> Self::F<Y> {
self.bind(|x| M::M::unit(f(x)))
}
}
fn main() {
let mx = Option::unit(0);
println!("{:?}", Functor::map(mx, |x| [x + 1, x + 2]));
}
Eine weitere, für das Verständnis wichtige, Funktion im
Zusammenhang mit Monaden ist join, die als
bind(id) definiert ist. Nun mag die Frage aufkommen,
warum man denn die identische Funktion id einsetzen
darf, wo die Signatur nichts über eine Selbstabbildung sagt.
Die Signatur ist hier
bind: (X -> M<Y>) -> M<X> -> M<Y>,
bzw. ohne Currying und in umgedrehter Reihenfolge
bind: (M<X>, X -> M<Y>) -> M<Y>.
Man darf hier nicht vergessen, dass die Typsignatur immer noch
eine polymorphe ist. Wir dürfen also
X = M<Y> verlangen. Das macht
bind: (M<M<Y>>, M<Y> -> M<Y>) -> M<Y>.
Nach Umbenennung Y:=X bekommt man
bind: (M<M<X>>, M<X> -> M<X>) -> M<X>.
Die Implementierung für Option:
fn join<X>(m: Option<Option<X>>) -> Option<X> {
m.bind(|x| x)
}
Mathematisch betrachtet ist eine Monade kodiert durch das Tripel
((Typkonstruktor, map), unit, join),bzw. abstrakt
(F, η, μ).
Hierbei ist F der Funktor. Die beiden Funktionen
η und μ sind natürliche
Transformationen.
Jede Monade muss die Axiome
μ∘F(μ) = μ∘μ, μ∘F(η) = μ∘η = id
erfüllen, bzw.
join ∘ map(join) = join ∘ join, join ∘ map(unit) = join ∘ unit = id.
Bei Option treten nur endlich viele Fälle
auf, die man jeweils nachrechnen kann.
Für join(mmx.map(join)) gilt
join(None.map(join)) = join(None) = None, join(Some(None).map(join)) = join(Some(join(None))) = join(Some(None)) = None, join(Some(Some(x)).map(join)) = join(Some(join(Some(x)))) = join(Some(x)) = x.
Bei join(join(mmx)) erhält man die gleichen
Ergebnisse
join(join(None)) = join(None) = None, join(join(Some(None))) = join(None) = None, join(join(Some(Some(x)))) = join(Some(x)) = x.
Für join(mx.map(unit)) gilt
join(None.map(unit)) = join(None) = None, join(Some(x).map(unit)) = join(Some(Some(x))) = Some(x).
Bei join(unit(mx)) erhält man die gleichen Ergebnisse
join(unit(None)) = join(Some(None)) = None, join(unit(Some(x))) = join(Some(Some(x))) = Some(x).