Das kartesische Produkt zweier Listen lässt sich unschwer als Komprehension entsprechend der mathematischen Definition formulieren:
def prod2(a, b):
return [(x, y) for x in a for y in b]
Bei dieser Formulierung dürfen a und b
allgemeiner iterierbare Objekte sein. Darüber hinaus gestattet die
Anpassung
def prod2_iter(a, b):
return ((x, y) for x in a for y in b)
die Einsparung von Speicher, dergestalt dass das Produkt nur einmal durch den erzeugten Iterator durchlaufen wird, dabei aber nicht als Ganzes im Speicher vorliegen muss.
Sind a und b geordnet,
ist die Auflistung lexikographisch geordnet.
Eine allgemeine variadische Formulierung erhält man gemäß der üblichen rekursiven Definition des Produktes:
def prod(*args):
if len(args) == 0:
return [()]
else:
return prod2(args[0], prod(*args[1:]))
Allerdings vererbt sich die rekursive Darstellung hierdurch auf
die Tupel. Obwohl man Tupel in der Mathematik rekursiv auf diese
Weise als Verschachtelung von Paaren definieren kann, wollen wir uns
hier lieber um flache Tupel bemühen. Man kann dies erreichen, indem die
folgende Operation flatten hinter den Rekursionsschritt
geschaltet wird.
def flatten(a):
return [(x,) + y for (x, y) in a]
def prod(*args):
if len(args) == 0:
return [()]
else:
return flatten(prod2(args[0], prod(*args[1:])))
Die seltsam anmutende Notation (x,) stellt ein
1-Tupel dar. Das Komma kommt am Ende hinzu, damit ein
syntaktischer Unterschied zur Prioritätsklammerung besteht.
Zur Optimierung expandieren wir noch flatten und
prod2 gemäß ihrer Definition. Es findet sich schließlich:
def prod(*args):
if len(args) == 0:
return [()]
else:
return [(x,) + y for x in args[0] for y in prod(*args[1:])]
Die Standardbibliothek enthält eine optimierte Implementierung der
lexikographischen Auflistung des kartesischen Produktes im Modul
itertools unter der Bezeichnung product.
Sie erzeugt der Erwartung entsprechend Iteratoren. Die kartesische
Potenz zum Exponent n schreibt man
product(a, repeat = n).
Beispielsweise gilt
product(a, repeat = 4) = product(a, a, a, a).
Der Raum der Abbildungen von X nach Y
lässt sich wie folgt erzeugen. Sei n = len(X).
Zunächst konstruiert die kartesische Potenz von Y
zum Exponent n den Raum der Abbildungen von
range(0, n) nach Y als Liste von
Tupeln. Zippt man nun den Definitionsbereich X mit
dem jeweiligen Tupel t, entsteht der Graph der
Funktion als Liste der Paare (X[k], t[k])
für k in range(0, n).
Kurzes Beispiel:
X = ["a", "b"]; Y = [0, 1]
product(Y, repeat = 2) = [(0, 0), (0, 1), (1, 0), (1, 1)]
zip(X, (0, 0)) = [("a", 0), ("b", 0)]
zip(X, (0, 1)) = [("a", 0), ("b", 1)]
zip(X, (1, 0)) = [("a", 1), ("b", 0)]
zip(X, (1, 1)) = [("a", 1), ("b", 1)]
Der Algorithmus zur Erzeugung des Raums ist insofern schlicht:
def mappings(X, Y, conv = list):
return [conv(zip(X, t)) for t in product(Y, repeat = len(X))]
Das optionale Argument conv gestattet die Festlegung
einer frei konstruierbaren Konvertierung des jeweiligen Graphen in
eine gewünschte Darstellung. Es bestehen unter anderem die
folgenden Darstellungen:
mappings(X, Y, list)
mappings(X, Y, dict)
mappings(X, Y, set)
mappings(X, Y, fn)
def fn(it):
d = dict(it)
return lambda x: d[x]
Für die Erzeugung eines Raums mehrstelliger Abbildungen genügt es, für den Definitionsbereich das entsprechende kartesische Produkt einzufügen. Das Programm
X = list(product([0, 1], repeat = 2))
Y = [0, 1]
for f in mappings(X, Y):
print(f)
beschreibt beispielsweise die Auflistung der 16 zweistelligen.
Eine endliche Abbildung ist genau dann injektiv, wenn ihr Definitionsbereich gleichmächtig zu ihrer Bildmenge ist. Der Raum der Injektionen ließe sich demnach erzeugen, indem bei der Erzeugung des Raums der Abbildungen diejenigen verworfen werden, bei denen diese Gleichmächtigkeit nicht besteht. Dies lässt sich folgendermaßen bewerkstelligen:
def injections(X, Y, conv = list):
return [conv(zip(X, t)) for t in product(Y, repeat = len(X))
if len(X) == len(set(t))]
Es ist jedoch effizienter, schlicht die Auflistung der Variationen zu nutzen:
from itertools import permutations
def injections(X, Y, conv = list):
return [conv(zip(X, t)) for t in permutations(Y, len(X))]
Beispielsweise berechnet das Programm
def S(X):
return injections(X, X)
print([len(S(range(n))) for n in range(8)])
die ersten Fakultäten.
Eine rekursive Ausführung von permutations
gelingt mit:
def permutations(a):
return [()] if len(a) == 0 else [(a[i],) + t
for i in range(len(a))
for t in permutations(a[0:i] + a[i+1:])]
Allgemeiner berechnet
def permutations(a, k):
return [()] if k == 0 else [(a[i],) + t
for i in range(len(a))
for t in permutations(a[0:i] + a[i+1:], k - 1)]
die Variationen der Länge k.
Zur Erzeugung des Raums der Kombinationen steht die Funktion
combinations aus dem Modul itertools
zur Verfügung. Der Aufruf combinations(a, k)
erzeugt die k-elementigen Teilmengen von a
in Form von Tupeln. Beispielsweise erzeugt
from itertools import combinations print(list(combinations([0, 1, 2], 2)))
die Ausgabe:
[(0, 1), (0, 2), (1, 2)]
Die rekursive Erzeugung geht auf dieselbe Weise vonstatten wie der Beweis der Übereinstimmung des Binomialkoeffizienten mit der Anzahl der Kombinationen. Das Argument ist Induktion über die Paare (n, k). Gesucht seien also die k-elementigen Teilmengen einer Menge Y mit n = |Y|. Im Anfang k = 0 gibt es genau eine Kombination, nämlich die leere Menge. Im Anfang k = n gibt es ebenfalls eine Kombination, nämlich die Menge Y selbst. Im Induktionsschritt nimmt man ein beliebiges Element y aus der Menge Y heraus, an welchem eine Fallunterscheidung vorgenommen wird. Entscheidet man sich, das Element y hinzuzufügen, verbleiben die (k−1)-elementigen Teilmengen von Y\{y} zu erzeugen. Entscheidet man sich dagegen, verbleiben die k-elementigen Teilmengen von Y\{y} zu erzeugen. Es entsteht der folgende Algorithmus:
def combinations(Y, k):
if k == 0:
return [set()]
elif k == len(Y):
return [Y]
else:
Y_minus_y = Y.copy(); y = Y_minus_y.pop()
C_take = [{y} | C for C in combinations(Y_minus_y, k - 1)]
C_skip = combinations(Y_minus_y, k)
return C_take + C_skip
Fast mühelos findet sich eine Anpassung, die mit Tupeln oder Listen anstelle von Mengen arbeitet:
def combinations(a, k):
if k == 0:
return [()]
elif k == len(a):
return [tuple(a)]
else:
c_take = [(a[0],) + c for c in combinations(a[1:], k - 1)]
c_skip = combinations(a[1:], k)
return c_take + c_skip
Die Auflistung geht hierbei lexikografisch geordnet
vonstatten, sofern a geordnet ist.
Die Potenzmenge von X ist definiert als die Menge der Teilmengen von X. Zu jeder Teilmenge A ⊆ X gehört genau eine Indikatorfunktion
1A(x) := 1 wenn x ∈ A, sonst 0.
Liegt umgekehrt die Indikatorfunktion der Teilmenge A vor, kann die Teilmenge per Komprehension
A = {x ∈ X | 1A(x) = 1}
zurückgewonnen werden. Zwischen der Potenzmenge und der Menge der Indikatorfunktionen besteht also eine natürliche Eins-zu-eins-Beziehung. Die Menge der Indikatorfunktionen ist aber nichts anderes als die Menge der Abbildungen X → {0, 1}. Das heißt, die Konstruktion der Potenzmenge lässt sich auf die Konstruktion des Raums der Indikatorfunktionen zurückführen.
Die Implementierung:
def power_set(X, conv = list):
return [conv(x for x in X if indicator[x] == 1)
for indicator in mappings(X, [0, 1], dict)]
Alternativ erhält man die Potenzmenge als Vereinigung aus jeder Menge der k-elementigen Teilmengen, wobei k von k = 0 bis k = |X| läuft. Weil die Mengen disjunkt sind, genügt ihre Konkatenation.
from itertools import combinations
def power_set(X, conv = list):
return [conv(x) for k in range(len(X) + 1)
for x in combinations(X, k)]
Die so erzeugte Potenzmenge ist der Größe nach und je Größe lexikographisch geordnet.
Zur Berechnung der Potenzmenge findet sich aber auch ein in direkter Weise rekursiver Algorithmus. Analog zu
2n+1 = 2⋅2n = (1 + 1)⋅2n = 2n + 1⋅2n
überlegt man sich für x ∉ X die Umformung
P(X ∪ {x})
≃ P({x})×P(X) = {∅, {x}}×P(X)
= ({∅} ∪ {{x}})×P(X)
= {∅}×P(X) ∪ {{x}}×P(X)
≃ P(X) ∪ {{x} ∪ A | A ∈ P(X)}.
Es ist unschwer zu bestätigen, dass die Gleichung
P(X ∪ {x}) = P(X) ∪ {{x} ∪ A | A ∈ P(X)}
in exakter Weise gilt. Man gelangt zu:
def power_set(X):
if len(X) == 0:
return [set()]
else:
x = X[-1]; P = power_set(X[:-1])
return P + [{x} | A for A in P]
bzw.
def power_set(X):
if len(X) == 0:
return [[]]
else:
x = X[-1]; P = power_set(X[:-1])
return P + [A + [x] for A in P]
Umwandlung in einen iterativen Algorithmus führt zu:
def power_set(X):
acc = [[]]
for x in X:
for A in acc.copy():
acc.append(A + [x])
return acc
Die innere Schleife ließe sich noch durch extend
beschreiben:
def power_set(X):
acc = [[]]
for x in X:
acc.extend(A + [x] for A in acc.copy())
return acc
Statt das Hilfsmittel acc.copy() oder
acc[:] zu verwenden, ginge auch:
def power_set(X):
acc = [[]]
for x in X:
acc.extend([A + [x] for A in acc])
return acc
Die Berechnung des Binomialkoeffizienten erfolgt günstig über dessen Produktformel, was zum Algorithmus
def bc(n, k):
if n < k: return 0
if n < 2*k: k = n - k
acc = 1
for i in range(1, k + 1):
acc = acc*(n + 1 - i)//i
return acc
führt. Man beachte, dass die Ganzzahldivision in der Schleife niemals einen Rest lässt.
Die Bernoulli-Zahlen lassen sich mit der Rekursionsformel
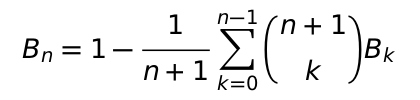
berechnen. Das Vorkommen von Bruchzahlen wird hierbei durch den
Typ Fraction berücksichtigt, wobei es genügt, den
Basisfall in diesen Typ umzuwandeln, da dies die restlichen
Operationen mit infiziert. Die Rekursion benötigt
überdies unbedingt eine Memoisierung.
from fractions import Fraction
def memoize(f):
memo = {}
def f_memo(n):
if not n in memo: memo[n] = f(n)
return memo[n]
return f_memo
@memoize
def B(n):
if n == 0:
return Fraction(1)
else:
return 1 - sum(B(k)*bc(n + 1, k) for k in range(n))/(n + 1)
Bei manchen kombinatorischen Problemen ist die Größe von Urbildern zu ermitteln.
Eine endliche Abbildung f: X → Y lässt sich invertieren, indem durch einmaliges Durchlaufen des Definitionsbereichs ein Wörterbuch erzeugt wird. Das Wörterbuch soll jedem Element dessen Urbild zuordnen.
def inv(f, X):
d = {}
for x in X:
y = f(x)
if y in d:
d[y].append(x)
else:
d[y] = [x]
return d
Jede Abbildung zerlegt ihren Definitionsbereich in disjunkte Urbilder, die man auch als Äquivalenzklassen betrachten kann. Die Funktion
def projection(f, X):
finv = inv(f, X)
return lambda x: finv(f(x))
erstellt die Projektion, die einem Element ihre Äquivalenzklasse zuordnet.